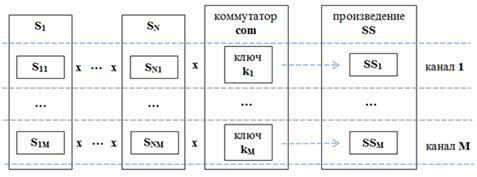
8.2. Произведение множеств состояний

Множество состояний SS называется произведением (непустых!) N множеств состояний

SS = (S1 × … × SN)k1, … ,kM  = ∏com(Si), (i = 1..N)

на M каналах (коммутации), образованных коммутатором из M  ключей

com = {k1, … ,kM}

которые являются состояниями одного массива (состояниями одного базиса), если:

• каждое из сомножителей Si, (i = 1..N) разбито на M непересекающихся подмножеств (сомножителей канала)
  Si = Si1 ⋃ … ⋃ SiM  = ⋃Sij, таких, что:
  
  • каждое состояние sij ∈ Sij одного канала Sij имеет соответствующий ему ключ kj в качестве своей проекции sij ⊵ kj, (i = 1..N, j = 1..M)
  • каждая N-ка состояний s1j , … , sNj, выделенных ключом kj из соответствующих множеств S1j , … , SNj, образует произведение (канал)
    s1j × … × sNj = ssj ∈ SSj ⊆ SS (то есть, каждый канал образован декартовым произведением элементов всех сомножителей этого канала)
• всё SS является объединением указанных каналов
  SS = Si1 ⋃ … ⋃ SiM
  то есть, каждый элемент ss ∈ SS является произведением некоторой N-ки состояний некоторого канала

Если M=0 (коммутатор отсутствует) или M=1, то такое произведение называется полным (такое произведение образовано декартовым произведением состояний всех сомножителей).

Тем самым, к j-ому каналу относятся:

• kj - ключ, идентифицирующий этот канал (если имеется коммутатор)
• S1j ... SNj – подмножества состояний исходных сомножителей
• SSj - образованное множество порожденных состояний

Назад Вперёд