8.2. Multiple of sets of states
The set of states SS is called the multiple of the N sets of states
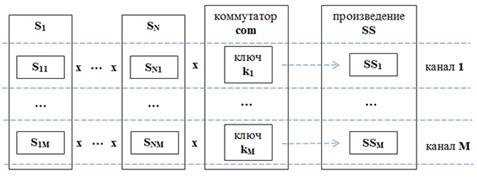
SS = (S1 × … × SN)k1, … ,kM = ∏com(Si), (i = 1..N)
on M channels (switching) formed by the switch from M keys
com = {k1, … ,kM}
which are the states of one basis if:
-
each of the
cofactors
Si,
(i = 1..N) is divided into
M
disjoint subsets
(factors of the channel)
Si = Si1 ⋃ … ⋃ SiM = ⋃Sij, such that:- each state sij ∈ Sij of one channel Sij has a corresponding key kj as its projection sij ⊵ kj, (i = 1..N, j = 1..M)
-
each
N
states
s1j
, … , sNj, allocated with the
key
kj from the corresponding
sets
S1j
, … , SNj, forms a
multiple
(channel)
s1j × … × sNj = ssj ∈ SSj ⊆ SS
-
all
SS is a
union of the specified
channels
SS = Si1 ⋃ … ⋃ SiM
that is, each element of ss ∈ SS is a multiple of some N states of some channel
If the number of states in each set Si, (i = 1..N) equal to M, then such a multiple is called the minimum.
If M = 1, then this multiple is called complete.
A special case of the
complete multiple is the absence of
keys in the
switch
com = ∅
Thus, the channel j includes:
- kj - key that identifies this channel
- S1j ... SNj – a subset of the original factors
- SSj - generated set of states
If some of the factors are empty sets, they simply do not participate in the formation of the multiple. If the empty sets are all factors, then their multiple is also an empty set.
█