9.17. Теорема

Пусть имеются три дерева T⚪, T* и T◎ такие, что:

• T⚪ является проекцией T◎
• пара вершин nd⫯ и nd⫰ принадлежат все трём деревьям
• в T⚪ вершины nd⫯ и nd⫰ являются соподчинёнными
• в T◎ между nd⫯ и nd⫰ имеется более одной промежуточной вершины, возможно, являющиеся корнями поддеревьев, в том числе некая вершина nd* (с единственной выходящей дугой, начинающей путь к вершине nd⫰)
• дерево T* отличается от T◎ только отсутствием вершины nd*, что связывает его с T◎ элементарным шагом типа Г, то есть, T* также является проекцией T◎

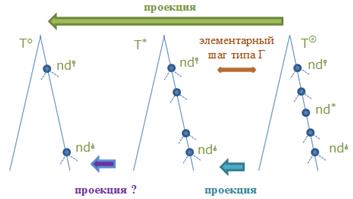
В этом случае T* также является проекцией T⚪.

Доказательство

Тем самым, надо доказать

1. ND⚪ ⊆ ND* (множество ND⚪ вершин дерева T⚪ является подмножеством ND* вершин дерева T*); это очевидно выполняется
2. если (ndb, nde) - дуга T⚪, то в T* существует путь (ndb, nde) между концами этой дуги; это также очевидно выполняется
3. если nd0 - ближайшая общая вершина для nd1 .. ndN дерева T⚪, то она является таковой для них и в T*, что доказывается следующим набором утверждений:
   • в T◎, являющимся прообразом T⚪, nd0 также - это ближайшая общая вершина для nd1 .. ndN
   • nd0 в T◎, очевидно, не может совпадать с nd*;
   • по условиям элементарного шага типа Г, связывающего T* и T◎:
     • такая вершина nd0 принадлежит также и дереву T*,
     • кроме nd0 никакая другая вершина nd0* дерева T* не может быть ближайшей для указанных nd1 .. ndN, поскольку в противном случае именно такая nd0*, очевидно, была бы ближайшей для них и в T◎

█

Назад Вперёд