10.7. Фрейм. Теорема
Пусть даны дерево T и множество ND = {nd1 .. ndN} из N>1 его вершин, попарно не лежащих на одном пути к корню.
Тогда существует единственное дерево FRAME, называемое фреймом на (указанных) вершинах, которое:
- является суммой ячеек c1 .. cM дерева T
- FRAME = ∑ci, (i=1..M)
- листьями которого служат указанные вершины ND (nd1 .. ndN служат листья базовых ячеек FRAME)
Доказательство
Cледующий алгоритм построения фрейма FRAME (отношения между вершинами nd1 .. ndN):
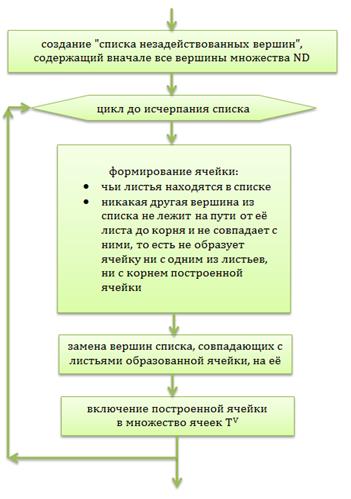
Для дерева T конечной высоты и некоторого множества выделенных вершин такой алгоритм завершается за конечное число шагов поскольку:
- образуемая ячейка существует согласно следующему алгоритму построения ячейки, входом для которого является текущее состояние "списка незадействованных вершин"
- на каждом шаге цикла количество вершин в списке уменьшается
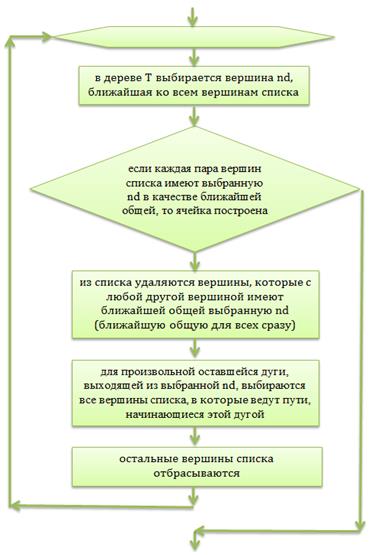
Полученное множество ячеек FRAME является суммой поскольку
- их корни и листья очевидно не совпадают
- корень только одной из них (последней по построению) не совпадает ни с одним листом никакой другой
- у всех прочих (если такие ячейки существуют) корни совпадают ровно с одним из листьев ровно одной другой ячейки, поскольку построенный корень замещает листья и участвует в качестве потенциального листа при построении новой ячейки
Доказательство единственности
Предположим обратное - существование другого дерева T*= <ND*, A*> с тем же набором листьев, которое также является проекцией T◎ согласно определению суммы.
Рассмотрим всевозможные пары (T_V,T_*) их различающихся поддеревьев, однако обладающих одинаковыми наборами листьев.
Для детального рассмотрения выберем такую пару, в которых хотя бы у одного члена (пусть, для определённости - у первого) нет поддерева, совпадающего с поддеревом некоторой другой из этих пар (оно само является "минимальным"), а затем докажем, что такой пары существовать не может, поэтому не могут существовать пары и с поддеревьями большей высоты, а значит, не верно предположение о существовании самого T*.
Вначале сразу укажем, что у T_V и T_* должен совпадать состав вершин, непосредственно подчинённых их корням, поскольку в противном случае у них был бы разный состав листьев. А согласно предположению о "минимальности" T_V следует совпадение тех поддеревьев, чьими корнями являются эти вершины.
Но у набора вершин, играющих роль листьев ячейки, может быть только один корень (ячейки), играющий согласно определению суммы роль корней T_V и T_*, что опровергает их различие между собой, а значит и само существование T_*. █
Замечание 10.1
Иначе говоря, при образовании множество вершин FRAME вначале копируются выделенные вершины ND дерева T, к которым затем добавляются те узлы T, которые являются ближайшими общими для уже включённых в указанное множество. █