12.3. Отношение проекции-прообраза между ВС
Вариативная ситуация vs⚪ называется (ВС-)проекцией ВС vs◎
vs◎ ⊵ vs⚪ или vs⚪ ⊴ vs◎
а та – её (ВС-)прообразом, если для каждого состояния s⚪ ∈ vs⚪ найдется его прообраз s◎ ∈ vs◎:
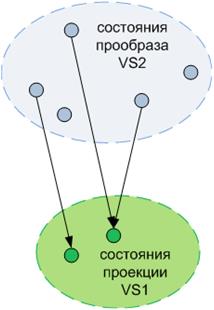
Это, в частности, подразумевает, что базис vs⚪ не шире базиса vs◎.
Будем также говорить, что vs⚪ и vs◎ находятся в отношении проекции-прообраза. █
Замечание 12.2
Если прообраз ВС рассматривать конкретизированную версию текущей ВС, то можно считать, что переход к нему обладает свойством монотонности, поскольку в этом случае:
- сохраняется множество её старых состояний и отношение ЛИБО между ними.
- в этих (старых) состояниях сохраняются их (старые) атомы и отношения И между ними.
В русле так понимаемой монотонности далее будет рассматриваться и развитие знаний о системах ВС, а также их версиях в виде модулей и сборок.
Замечание 12.???
У состояний из vs⚪ множества их прообразов в vs◎ не пересекаются.
Если бы это было не так, то имелось бы некое состояние s◎ в vs◎, имеющее проекцией как минимум пару состояний s1⚪ и s2⚪ из vs⚪.
Но эти состояния находятся в отношении ЛИБО, то есть их формирует в том числе хотя бы одна переменная v, которая имеет для них разные значения.
Эта же переменная должна формировать и s◎, но её значения оказывается противоречивым, что доказывает ложность исходного предположения о наличии в vs◎ указанного состояния s◎.