17.2. Теорема

Пусть даны основы двух согласованных с ними систем ВС

[SVS◎] = <T◎, COM◎, SEL◎, VS⧋◎, VS⫧◎> и связанная с ней одним из ЭШ типа Б или ЭШ типа В её О-проекция

[SVS⚪] = <T⚪, COM⚪, SEL⚪, VS⧋⚪, VS⫧⚪>

такие, что отличие между ними согласно замечанию 1 заключается в замене некоторой системообразующей ВС на её ВС-прообраз, что приводит к изменениям в ряду вышестоящих ВС.

То есть, предположив, что для произвольной пары ВС из такого ряда:

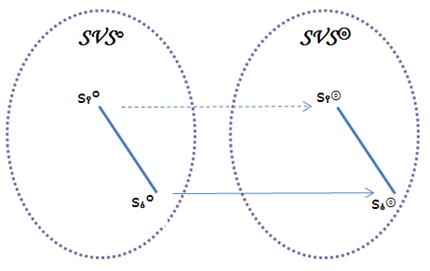
• деревьям T◎ и T⚪ принадлежат некий узел nd⫯ и непосредственно подчинённая ему вершина nd⫰
• vs⫯⚪ из VS⚪ и vs⫯◎ из VS◎, а также vs⫰⚪ из VS⚪ и vs⫰◎ из VS◎ – ВС, сопряженные соответственно с nd⫯ и nd⫰
• vs⫰◎ – произвольный ВС-прообраз vs⫰⚪,

  vs⫰⚪ ⊴ vs⫰◎

Тогда vs⫯◎ - также ВС-прообраз vs⫯⚪

vs⫯⚪ ⊴ vs⫯◎

Доказательство

Согласно определению 12.3 надо доказать, что для каждого состояния s⫯⚪ ∈ vs⫯⚪ найдется его прообраз s⫯◎ ∈ vs⫯◎.

В зависимости от типа узла nd⫯:

1. nd⫯ имеет тип ЛИБО;
   1. SVS⚪ согласована, а значит, в vs⫰⚪ существует некое состояние s⫰⚪, являющееся проекцией s⫯⚪, поскольку такое s⫯⚪ является произведением s⫰⚪ и ключа k ∈ sel из SEL, сопряженного с дугой (nd⫯ , nd⫰):

      s⫯⚪ = s⫰⚪ × k

   2. в vs⫰◎ существует некое состояние s⫰◎, являющееся проекцией s⫰⚪.

      s⫰◎ = s⫰⚪ × s⫰◎

   3. s⫯◎ является произведением s⫰◎ и того же самого k (по определению О-проекции)

      s⫯◎ = s⫰◎ × k =

      = (s⫰⚪ × s⫰◎) × k =

      = (s⫰⚪ × k) × s⫰◎ =

      = s⫯⚪ × s⫰◎

   тем самым, являясь прообразом s⫯⚪, что и требовалось доказать

2. nd⫯ имеет тип И;
   1. SVS⚪ согласована, а значит, в vs⫰⚪ существует некое состояние s⫰⚪, являющееся проекцией s⫯⚪, поскольку s⫯⚪ является произведением:
      • некоторого и ключа k ∈ com из COM (может отсутствовать), сопряженного с узлом nd⫯
      • состояния s⫰⚪
      • некоторых состояний s1⚪ .. sM⚪ из прочих ВС, сопряженных с остальными вершинами, непосредственно подчинёнными узлу nd⫯, и также имеющими произведение с ключом k

        s⫯⚪ = k × s⫰⚪ × s1⚪ × .. × sM⚪

   2. s⫰◎ = s⫰⚪ × s⫰◎
   3. s⫯◎ является произведением:
      • того же самого k
      • состояния s⫰◎
      • тех же самых состояний s1⚪ .. sM⚪ (согласно замечанию 1)

        s⫯◎ = s⫰◎ × k × s1⚪ × .. × sM⚪ =

        = (s⫰⚪ × k) × s⫰◎ × s1⚪ × .. × sM⚪ =

        = s⫯⚪ × s⫰◎ × s1⚪ × .. × sM⚪

      тем самым, являясь прообразом s⫯⚪, что и требовалось доказать

█

Назад Вперёд