21.8. Алгоритм построения композиции деревьев

Основан на таком взгляде, согласно которому отношение смежности между вершинами дерева разбиения любой системы ВС могут пониматься не только как "непосредственное следование", но и как просто "следование" между теми же вершинами, но уже некоторой надсистемы, что основано на свойстве транзитивного замыкания включать в себя исходное отношение. Ранее это было формализовано в понятиях отношения прообраза-проекции деревьев и композиции деревьев.

Алгоритм получает на вход набор исходных деревьев

T1 = (ND1, A1),

..

TN = (NDN, AN)

в виде их матриц дуг

M1..MN

и используя теорему 21.2, согласно которой матрица путей такой суммы деревьев совпадает с транзитивным замыканием вычисленной суммы для отношений смежности исходных деревьев, последовательно решет 5 следующих друг за другом подзадач:

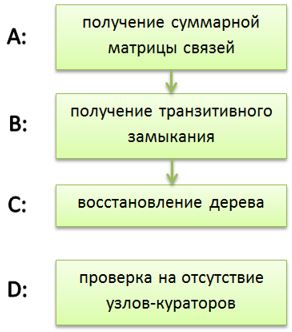
A. Алгоритм получения суммарной матрицы связей в чуть более подробном виде образован тремя шагами:

1. получение объединения множеств вершин всех исходных деревьев

ND = ND1 ⋃ .. ⋃ NDN

2. в базисе полученного множества ND производится перепостроение заново каждой матрицы дуг каждого исходного дерева

M1*..MN*

3. получение суммарной матрицы связей M∑ путём сложения в едином базисе заново построенных матриц дуг:

M∑ = M1* + .. + MN*

B. Получение матрицы путей 𝕄∑, выражающей отношение достижимости, заключается в выполнения транзитивного замыкания ранее построенной матрицы связей M∑, что может быть сделано, например, с помощью широко известного алгоритма Флойда — Уоршалла

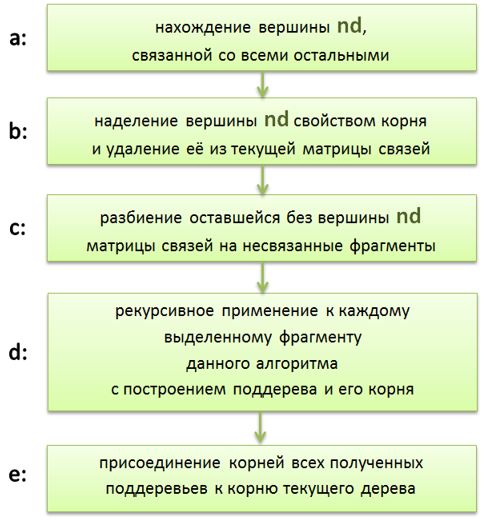
C. Алгоритм восстановления дерева T основан на трактовке отношения смежности, требуемого для явного определения T, как уже полученного в 𝕄∑ отношения достижимости с дополнительным условием отсутствия явно указанные промежуточных вершин; главная идея этого алгоритма использует то определение дерева, которое трактует его как граф, связывающий корень дугами с собственными поддеревьями:

Указанный в пункте D алгоритм недопущения узлов-кураторов служит цели обеспечить сохранность ближайших общих вершин исходных деревьев во вновь построенном. Соответственно он получает на вход одно из исходных T1 .. TN в виде матриц M1..MN и готовое дерево T в виде матрицы M, а возвращает логический признак корректности.

цикл по всем узлам ndj исходного Ti

цикл по всем дугам ak, выходящим (в Ti) из ndj

получение (в Ti) вершины nd*j – конца дуги ak

проверка, существует ли в T узел, лежащий на пути от ndj к nd*j;

при положительном результате

цикл по всем узлам nd^j, лежащим на пути от ndj к nd*j;

проверка, ведут ли (в T) из такого nd^j пути ещё какую-нибудь вершину Ti, кроме как в nd*j

положительный результат означает выход из алгоритма с признаком некорректности T на Ti

конец цикла

конец цикла

конец цикла

выход из алгоритма с признаком корректности T на Ti

Пункты a) и c) и D могут не иметь решения.

█

Назад Вперёд