11.20. Элементарный шаг преобразования каркаса типа Г

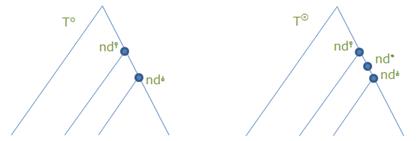
Пусть даны два корректных каркаса

SKEL⚪ = <T⚪, SH⚪, COM⚪, SEL⚪> и

SKEL◎ = <T◎, SH◎, COM◎, SEL◎>

такие, что:

• T◎ отличается от T⚪ лишь наличием дополнительной вершины nd* между двумя смежными вершинами nd⫯ и nd⫰ с соответствующей заменой дуги a=(nd⫯, nd⫰) на путь (nd⫯, nd*, nd⫰), то есть T⚪ и T◎ связаны элементарным шагом типа Г;

  

• для всех вершин дерева T⚪ кроме nd⫯, принадлежащих, естественно, и T◎, совпадают сопряжённые с ними коммутаторы и селекторы
• если вершина nd⫯ является узлом типа И, то сопряжённые с ней в SKEL⚪ и SKEL◎ коммутаторы совпадают
• если вершина nd⫯ является узлом типа ЛИБО, то у сопряжённых с ней в SKEL⚪ и SKEL◎ селекторов совпадают ключи, сопряжённые с теми дугами дерева T⚪, которые НЕ ведут непосредственно к вершинам nd* или nd⫰; в последнем случае ключи совпадают, но относятся к разным дугам – (nd⫯, nd⫰) в T⚪ и (nd⫯, nd*) в T◎
• если вершина nd* имеет тип И, то с ней в SKEL◎ сопряжён произвольный коммутатор, в том числе, он может быть пустым
• если вершина nd* имеет тип ЛИБО, то сопряжённый с ней в SKEL◎ селектор имеет единственный канал, соответствующий дуге (nd*, nd⫰)

В этом случае SKEL⚪ и SKEL◎ называются связанными элементарным шагом (преобразования) типа Г. █

Назад Вперёд