11.21. Теорема
Пусть даны два каркаса
SKEL⚪ = <T⚪, SH⚪, COM⚪, SEL⚪> и
SKEL◎ = <T◎, SH◎, COM◎, SEL◎>
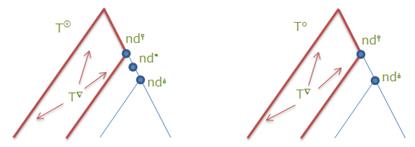
чьи деревья T⚪ и T◎ связаны элементарным шагом типа Г, то есть T◎ отличается от T⚪ лишь наличием дополнительной вершины nd* между двумя смежными вершинами nd⫯ и nd⫰ с соответствующей заменой дуги a = (nd⫯, nd⫰) на путь (nd⫯, nd*, nd⫰).
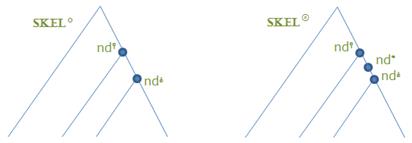
Если при этом SKEL◎ корректен на некотором множестве Sh0, то и SKEL⚪ также корректен на этом же множестве.
Доказательство
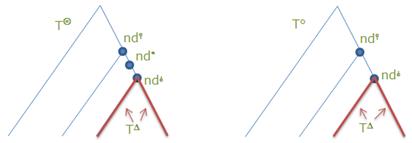
корректности каркаса, то есть существования для каждой вершины дерева T⚪ сопряжённого с ней множества унаследованных ключей nd⫯⚪, подчиняющегося отношению корректности, разбито на три части согласно представлению дерева T⚪ в виде суммы его основы T∆ и дополнения T∇, которые разделены вершиной nd* и которые совпадают в T⚪ и T◎:
-
Для доказательства первой части, то есть существования
корректно связанных
множеств
sh∇
∈
SH⚪, достаточно заметить их совпадение с
множествами
унаследованных ключей,
сопряжёнными с теми же
вершинами указанного
дерева
T∇, но уже из состава
T◎:
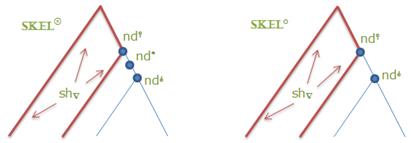
Отношение корректности между множествами унаследованных ключей sh∇ при этом сохраняется, поскольку зависит только от связей соподчинения в дереве T∇, которое одно и то же в SKEL⚪ и SKEL◎.
-
Вторая часть сама состоит из пары доказательств: во-первых, для
вершины
nd⫯, а затем – и для
вершины
nd⫰.
-
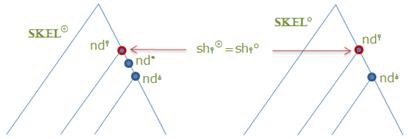
итак, вначале следует указать на совпадение
множеств
унаследованных ключей
sh⫯⚪
∈
SH⚪ и
sh⫯◎
∈
SH◎, которые
сопряжены с
вершиной
nd⫯ соответственно в
SKEL⚪ и
SKEL◎
sh⫯⚪ = sh⫯◎
-
Далее докажем, что независимо от
типа узла
nd⫯ имеется совпадение
множества
sh⊥⚪
∈
SH⚪ и
sh⊥◎
∈
SH◎, которые
сопряжены соответственно с
вершиной
nd* в
SKEL⚪ и с
вершиной
nd⫰ в
SKEL◎
sh⊥⚪ = sh⊥◎
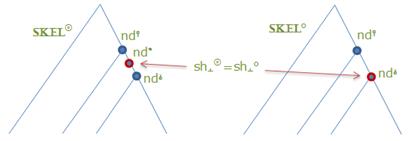
Это очевидно, поскольку для обеих вершин nd* и nd⫰ соответствующие множества sh⊥◎ и sh⊥⚪ образуются как произведение совпадающих множеств sh⫯⚪ и sh⫯◎ на одно и то же множество k ключей узла nd⫯ – ключей его селектора или ключей его коммутатора в зависимости от типа узла.
sh⊥⚪ = k ✖ sh⫯⚪
sh⊥◎ = k ✖ sh⫯⊚
Здесь важно то, что множество sh⊥⚪ являет проекцией множества sh⫰◎
-
итак, вначале следует указать на совпадение
множеств
унаследованных ключей
sh⫯⚪
∈
SH⚪ и
sh⫯◎
∈
SH◎, которые
сопряжены с
вершиной
nd⫯ соответственно в
SKEL⚪ и
SKEL◎
-
Доказательство третьей части проводится по индукции,
базисом которой служит только что доказанное утверждение существования
множества
sh⊥⚪,
корректно сопряжённого с
вершиной
nd⫰ из
T∆◎ , одного для
SKEL⚪ и
SKEL◎.
Теперь рассмотрим для указанного дерева T∆ произвольную пару соподчинённых вершин nd∧ и nd•, а также сопряжённые с ними множества sh∧◎, sh•◎, sh∧⚪ и sh•⚪ такие, что sh∧⚪ является проекцией sh∧◎:
sh∧◎ ⊵ sh∧⚪
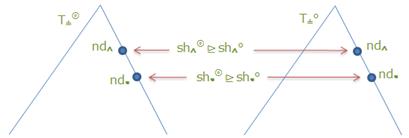
Здесь надо доказать, что sh•⚪, связанное отношением корректности с sh∧⚪ существует, являясь при этом проекцией sh•◎:
sh•◎ ⊵ sh•⚪
Это очевидно, поскольку sh•◎ и sh•⚪ являются произведениями соответственно sh∧◎ и sh∧⚪ на одно и то же множество k∧, образующих ключей селектор или ключей коммутатор в зависимости от типа узла nd∧:
sh•◎ = k∧ ✖ sh∧◎
sh•⚪ = k∧ ✖ sh∧⚪
Но первое из этих произведений (k∧ ✖ sh∧◎) существует, так как принадлежит корректному каркасу SKEL◎. Значит, существует и второе (k∧ ✖ sh∧⚪), что можно доказать от противного.
Пусть, например, в sh•⚪ имеется некая переменная v, принимающая разные значения: z1 в k∧ и z2 в sh∧⚪.
Но в этом случае такая переменная v с указанными значениями должна принадлежать также sh∧◎, поскольку это sh∧◎ является прообразом sh∧⚪.
Следовательно, sh•◎ также не может существовать, что противоречит условию. А это значит, что второе произведение sh•⚪ также существует, образуя с sh•◎ отношение корректности.
Тем самым доказано, что при заданных условиях существуют такие множества унаследованных ключей SH⚪, которые формируют корректный каркас SKEL⚪.
SKEL⚪ и SKEL◎ следовательно, также как и их деревья, сами связаны между собой элементарным шагом типа Г. █