18.12. Теорема

Пусть даны:

• согласованная система ВС

  SVS = <T, SH, COM, SEL, VS>

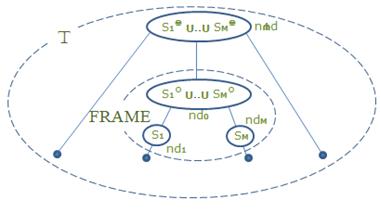
• фрейм FRAME её дерева T на выделенных вершинах

  {nd1 .. ndM } = ND

• базовые и/или частичные ВС vs1 .. vsM сопряжены с вершинами nd1 .. ndM
• к vs1 .. vsM принадлежат множества состояний S1 .. SM

Тогда утверждение о ЛИБО-сопряжённости указанных S1 .. SM равносильно утверждению о существовании ЛИБО-фрейма

<FRAME, S1 .. SM>

Доказательство

Вначале дадим развёрнутые определения, конкретизирующие условия теоремы

• согласно определению 11.3 ЛИБО-сопряжённость указанных S1 .. SM означает, что порождённые от них состояния S1◎ .. SM◎ корневой ВС vs⋔0 не пересекаются
• согласно лемме 18.4 и определение 18.5 ЛИБО-фрейма

  <FRAME, S1 .. SM>

  утверждают, что с его корнем nd0 сопряжена ВС vs0, содержащая непересекающиеся множества состояний S1⚪ .. SM⚪, порождённые от S1 .. SM.

Теперь требуется проверить два следующих утверждения:

1. из наличия ЛИБО-фрейма следует ЛИБО-сопряжённость указанных множества состояний, что верно, поскольку в согласованной системе из существования непересекающиеся множества состояний S1⚪ .. SM⚪ следует, что не пересекаются и все порождённые от них множества состояний в каждой вышестоящей, в том числе и корневой ВС vs⋔0 - S1◎ .. SM◎, которые тем самым порождённые и от S1 .. SM; то есть S1 .. SM являются ЛИБО-сопряжёнными, что и требовалось доказать
2. из ЛИБО-сопряжённости состояний S1 .. SM следует существование ЛИБО-фрейма, что верно, поскольку:
   1. существование в корневой ВС vs⋔0 непересекающихся множеств состояний S1◎ .. SM◎, порождённых от S1 .. SM, означает, что и в ВС, сопряжённой с корнем nd0 фрейма, соответствующие множества S1⚪ .. SM⚪, порождённые от S1 .. SM, также существуют и не пересекаются, так как у S1◎ .. SM◎ нет другого способа быть порождёнными от S1 .. SM
   2. далее по индукции используя результат теоремы 18.5 можно доказать, что для каждой ячейки указанного фрейма можно построить сопряжённую с ней ЛИБО- / И-ЛИБО-ячейку так, что в головных узлах соподчинённых ей ячеек будут существовать непересекающиеся множества состояний, порождённые от множеств соответствующего канала, что как-раз будет означать существование ЛИБО-фрейма, что и требовалось доказать.

█

Замечание 18.2

По сути, это другое определение косвенного (порождённого) отношения ЛИБО. █

Назад Вперёд