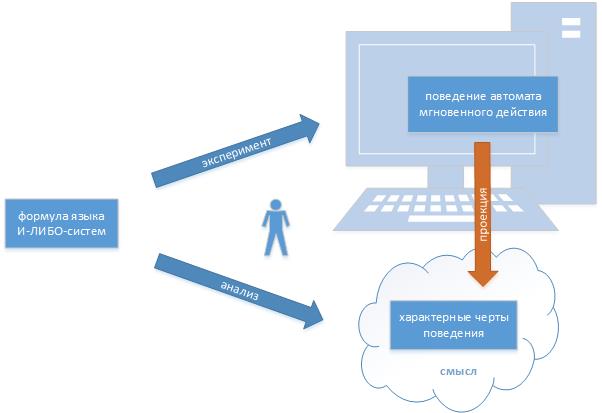
24.2 Смысл формулы
Для начала необходимо доказать тождество характерных черт согласованной системы и характерных черт поведения (Теорема 24.13), которые поэтому (здесь!) можно назвать двумя сторонами смысла:
- смысла формулы языка И-ЛИБО-систем, фиксируемого в характерных чертах согласованной системы
- смысла, заложенного в поведение того автомата мгновенного действия, чью конструкцию она непосредственно определяет в качестве значения
что позволяет конкретезировать общее понятие смысла: смысл = характерные черты (согласованной системы и/или поведения)
Если предметную область рассматривать как статическую, то для таких формул являются эквивалентными значение и смысл поскольку все фрагменты считаются корректны как в отношении дрг к другу, так и к их сумме.
Различие становится явным в случае динамики, когда некий модуль, описываемый своей формулой, начинае рассматриваться в ряду формул, описывающих всё более сложное его "окружение" с помощью И- и ЛИБО-соединений.

В правильном случае, этот смысл должен оставться инвариантом поведения, что обеспечивается именно в формулах, но не вообще записях.
Введение понятия собственно характерных черт согласованной системы здесь понадобилось для того, чтобы перевести обычно последовательное усложнение автомата в единый эксперимент с рядом всё более его сложнных версий, и при этом иметь буквально(!) одинаковые его смысловые характеристики - эти самые его характерные черты согласованной системы.
Строгое обоснование условий монотонности при таком подходе через тождество (характерных черт согласованной системы) и было целью работы.
То есть, собственно осмысленная (сложная) запись - это формула, что подразумевает её положительную проверку на соглассованность; в противном случае она бессмысленна (внутренне противоречива).
Можно чуть подробнее расшифровать сказанное в отношении сохранения характерных черт согласованной системы.
Для этого надо рассмотреть эксперимент с двумя автоматами, чьи описания в виде формул согласованных систем находятся в соотношении О-проекции.
Тогда в испытании таком, что активными являютя оба автомата:
- если для первого оно оказывается корректным, то и для второго также корректным (см. Теорема ...)
- если для первого характерные черты согласованной системы представлены неким множеством, то оно являетя подмножеством характерных черт согласованной системы второго (см. Теорема ...)
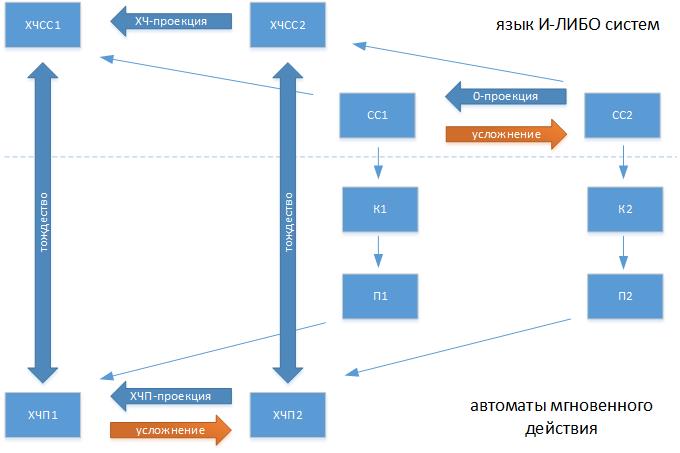
Пусть даны две согласованные системы - СС1 и СС2, находящиеся в отношении О-проекции.
Согласно Главной Теореме их характерные черты ХЧСС1 и ХЧСС2 должны также находиться в отношении проекции (ХЧ-проекции).
Однако, СС1 и СС2 описывают - непосредственно конструкции К1 и К2 неких автоматов, а косвевенно - их поведение П1 и П2.
Тогда их характерные черты поведения - ХЧП1 и ХЧП2, также находятся в отношении проекции в силу их тождества с ХЧСС1 и ХЧСС2 (Теорема 24.13).
То есть, успешные "статические" проверки позволяют утверждать, что и в "динамике" проводимые эксперименты сохраняют монотонность смыслов.
С той лишь разницей, что здесь "статика" существенно проще "динамики".
Поэтому, в идеале, разработчики смогут усложнять конструкцию и при этом быть уверенными, что и поведение "лишь" усложнится, а не приведёт к неожиданным ошибкам.
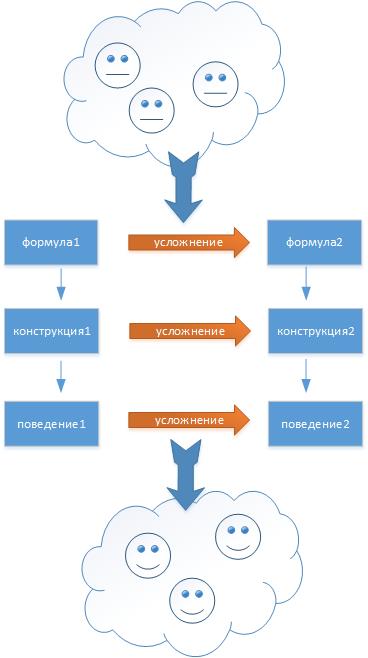
Здесь для начала рассматривается вопрос сравнения поведения, для чего эксперимент производится в одни и те же моменты времени сразу над двумя (корректными!) системами: s, а также над такой S, которя "включает" в себя s* - (конструктивную) "копию" s.
Конструкций две (s и s*), но их поведение ожидается совпадающим с точностью до взаимно-однозначного соответствия между двумя экземлярами их уникальных действий.
Это и должно служить критерием корректного усложнения, иначе говоря, монотонного, то есть сохраняющего смысл.
Очевидно, так понимаемый смысл образуется как инвариант расширяющегося контеста при описании всё более сложных надсистем:
- если в некотором испытании как s, так и s* активированы и s работает без ошибок, то и S должна работать штатно
- если в таком испытании системой s производятся действия д1..дн, которые очевидно связаны отношением одновременности так, что в эксперименте нет других испытаний, где присутствовала бы только часть из них, то таковыми они должны быть и для S
- если наоборот, в эксперименте группы действий {д1}..{дн} системы s принадлежат разным группам испытаний, то есть являются разновременными, то таковыми они должны быть и для S
Тем самым, намечаются основы того, далее будет определено как характерные черты согласованной системы (ХЧП) рассматриваемой системы s, иначе говоря - её смысл:
- значения входных переменных, при которых любая включающая её над-система S сама работает штатно, и при этом активирует рассматриваемую под-систему s*
- отношения одно- и разно- временности между группами действий s, наблюдаемых в любой её над-системе S